Wapening van ophoging door geokunststof - Methode P. Risseeuw

Wapening van ophoging door geokunststof

Ophogingen moeten zodanig ontworpen worden dat er geen gevaar bestaat voor bezwijken.

Hierbij worden drie typen onderscheiden: - uitwendig - inwendig - doorpersen

Voor elk van deze mechanismen wordt een berekeningsmethode gebruikt. Bij onvoldoende sterkte van de grond kan gebruik worden gemaakt van wapening door een geokunststof. De methoden zullen hier achtereenvolgens worden toegelicht.

Uitwendig bezwijken

Een helling van een ophoging kan onderuit gaan door afschuiven. Dit gevaar kan onderzocht worden via stabiliteit programmatuur. Hierbij worden aandrijvend en tegenwerkend moment afgeschat. Hun quotiënt bepaalt de mate van veiligheid. Hiervoor zijn talloze programma’s beschikbaar op de markt.

Als er onvoldoende veiligheid is, kan er gebruik gemaakt worden van een geokunststof. Hierin ontwikkelt zich bij dreigend afschuiven een trekkracht die het tegenwerkend moment positief beïnvloedt. Hierdoor wordt de veiligheid voldoende op peil gebracht. Doorsnee programmatuur bevat de mogelijkheid om een geokunststof mee te nemen in de berekening. Vaak is het handig in het voortraject van een ontwerp een snelle simpele schatting te kunnen maken van een benodigde geokunststof. Deze mogelijkheid wordt geboden in deze Applet. De aanpak is geïntroduceerd door Risseeuw.

Aanpak

De geschematiseerde geometrie is weergegeven in Fig. 1. De ondergrond is bruinachtig weergegeven, de ophoging gelig. De van belang zijnde maten zijn aangegeven. Het glijdvlak is cirkelvormig. Langs het deel in de ondergrond heerst een ongedraineerde schuifspanning c_u. Langs het deel in de ophoging geven we de schuifspanning aan met τ_a . Deze laatste schuifspanning hangt af van het materiaal van de ophoging en de toestand bij punt D. Bij een wrijvingsmateriaal speelt de wrijvingshoek een rol, bij een cohesief materiaal de cohesie. Vaak is de ophoging gescheurd bij punt D. Het wordt aan de gebruiker overgelaten om een goede schatting te maken van de effectieve schuifspanning τ_a. Het gewicht van de ophoging wordt bepaald door het soortelijk gewicht γ_a. Voor de eenvoud wordt gewerkt met totaalspanningen.

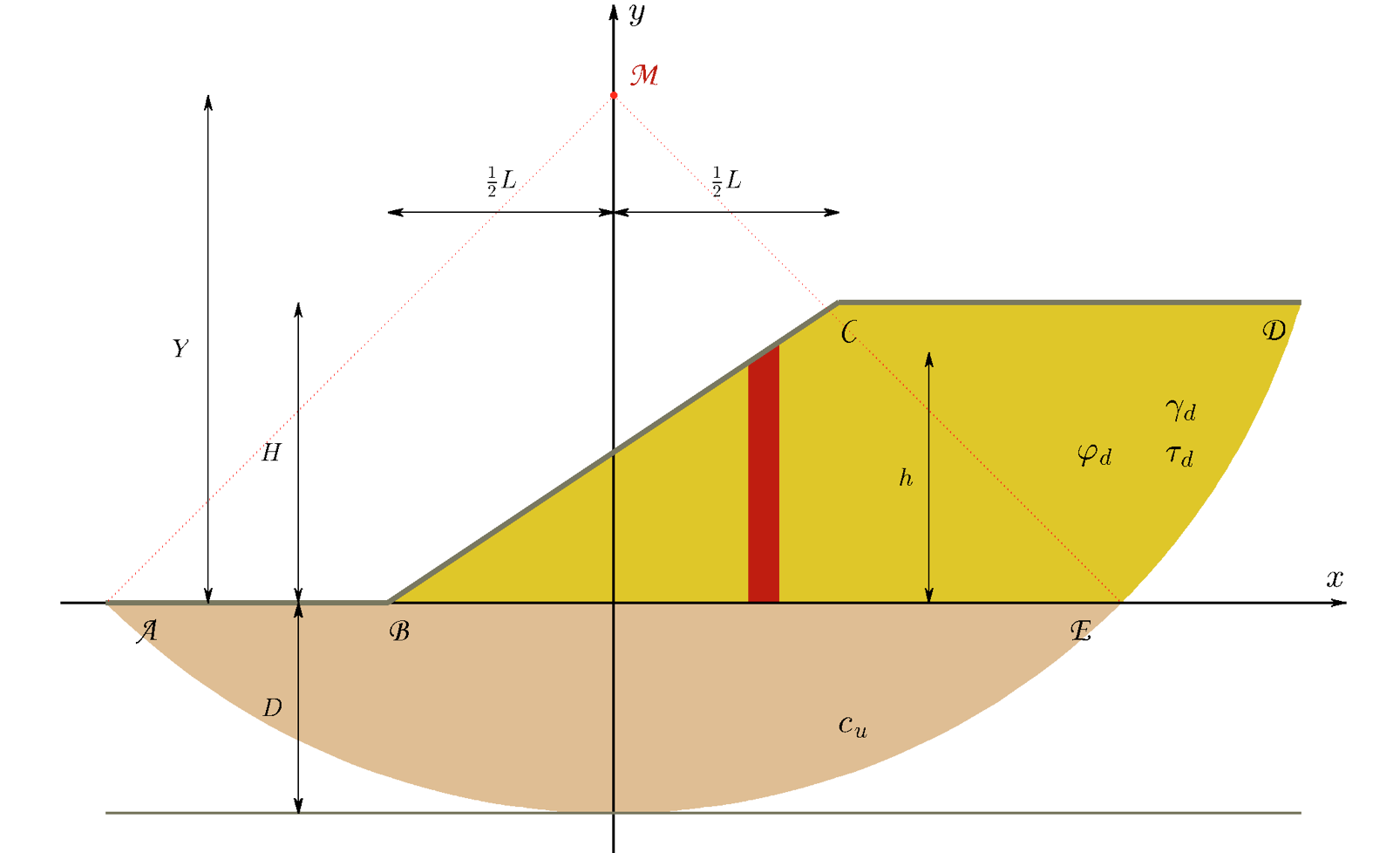
Bij stabiliteitsberekeningen wordt gezocht naar de glijdcirkel, waarvoor de kleinste veiligheidscoëfficiënt geldt. Daarvoor is een computerprogramma nodig. Het doel hier is een eenvoudige snelle bepaling. Daarom wordt de cirkel gekozen op basis van ervaring. Risseeuw stelt dat het middelpunt van de cirkel midden boven het talud ligt, dat hoek AME 90˚ bedraagt en dat de straal van de cirkel zo groot is dat de vaste ondergrond net geraakt wordt. In formulevorm

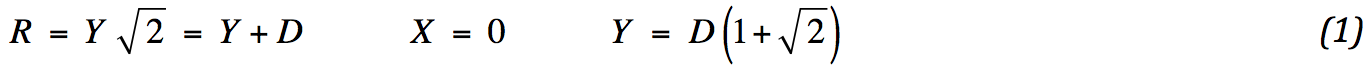
Voor een extreem dunne ondergrond is deze aanpak minder realistisch. De stabiliteitsmethodiek werkt niet, als de glijdcirkel terug loopt. We moeten ervoor zorgen dat Y > H . Om complicaties in de berekening te voorkomen zou het fijn zijn, als punt E rechts van punt C ligt. Dan moet worden voldaan aan

Dit is geen onredelijke beperking.

Uitwerking

Bij stabiliteitsberekeningen wordt de veiligheidscoëfficiënt uitgedrukt als het quotiënt van aandrijvend en tegenwerkend moment. In de huidige aanpak wordt het aandrijvend moment geleverd door het gewicht van de ophoging. Het gewicht van de ondergrond speelt geen rol, omdat de resulterende bijdrage wegvalt. De straal van de glijdcirkel is Y √2 . Het tegenwerkend moment bestaat uit drie bijdragen: de ongedraineerde schuifspanning langs de kwart cirkelboog, de schuifspanning in de ophoging langs de rest van de boog en trekkracht in de geokunststof S. Er geldt:

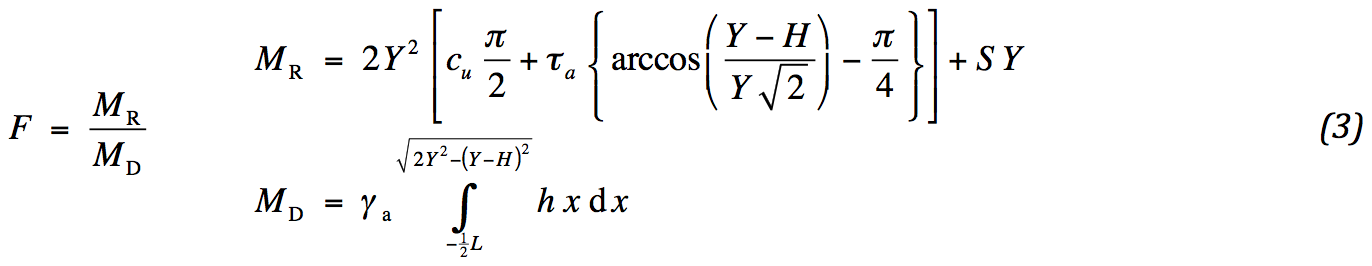
In het aandrijvend moment wordt het verloop van de hoogte verwerkt. Deze wordt overgenomen uit Fig. 1. Voor de integralen bestaat een gesloten oplossing. De grenzen worden aangegeven als stokterm:

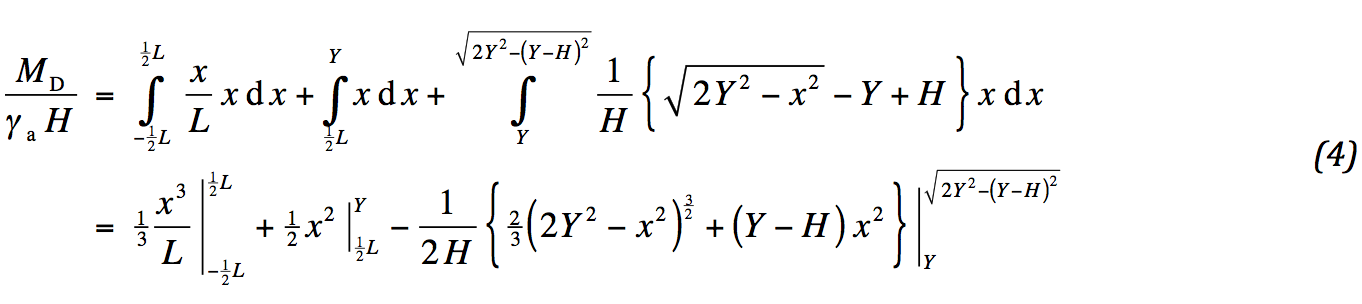
Invullen van de grenzen leidt tot:

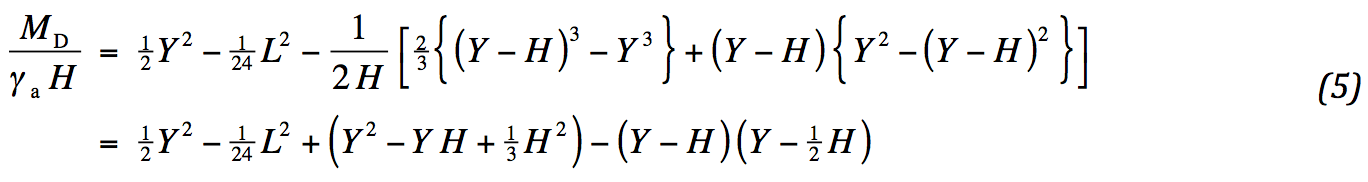
Het uiteindelijke resultaat blijkt relatief eenvoudig:

Hiermee is de benodigde trekkracht in de geokunststof vastgelegd voor een gewenste veiligheidscoëfficiënt. Uit (3) en (6) volgt:

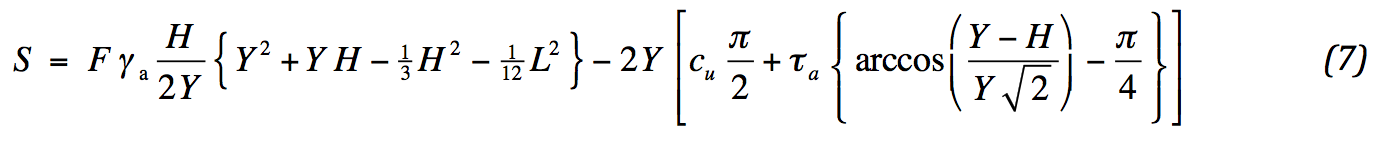
Een geokunststof is gewenst bij een positieve waarde van (7)

Inwendig bezwijken

Een helling van granulair materiaal is stabiel tot de hoek ervan overeen komt met de interne wrijvingshoek. Hierbij ontstaat een spanningstoestand, waarbij zich op een horizontaal vlak schuifspanningen zullen ontwikkelen. Dit betekent dat de ondergrond in staat moet zijn dergelijke schuifspanningen te weerstaan. Daartoe moet de ongedraineerde schuifsterkte ervan voldoende groot zijn.

Indien dit niet het geval is, kan een geokunststof toegepast worden om het verschil te overbruggen. Het bepalen van de benodigde sterkte is geen eenvoudige zaak. De spanningstoestand rond de helling is ingewikkeld. Helling en wrijving langs de kunststof spelen onder meer een rol. Daarnaast is de overgang naar de ondergrond complicerend. Daarom heeft Risseeuw het probleem vanuit een ander conservatief standpunt bekeken. In het midden van de ophoging heerst ongeveer een zogenaamde actieve horizontale gronddruk. Deze druk zal op de een of andere manier bij de helling afgevoerd moeten worden naar de ondergrond. Als nu aangenomen wordt, dat de wrijving langs de geokunststof de gronddruk kan compenseren, dan is het voldoende te eisen dat de kuststof deze sterkte heeft. In formulevorm:

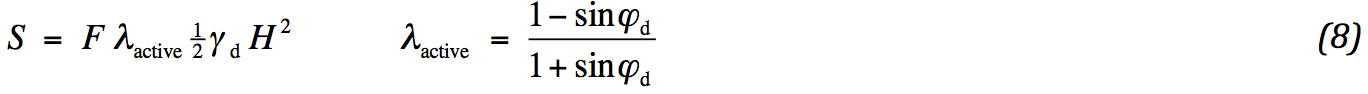
Een veiligheidsfactor is toegevoegd. Helling en ongedraineerde schuifsterkte zitten niet in deze formule. Het kan best zijn dat voor voldoende kleine helling of grote schuifsterkte geen geokunststof vereist is. Daarom is de formule conservatief. Ook speelt de wrijving langs de kunststof geen rol. Dit betekent een onzekerheid of de gronddruk wel geheel afgevoerd kan worden.

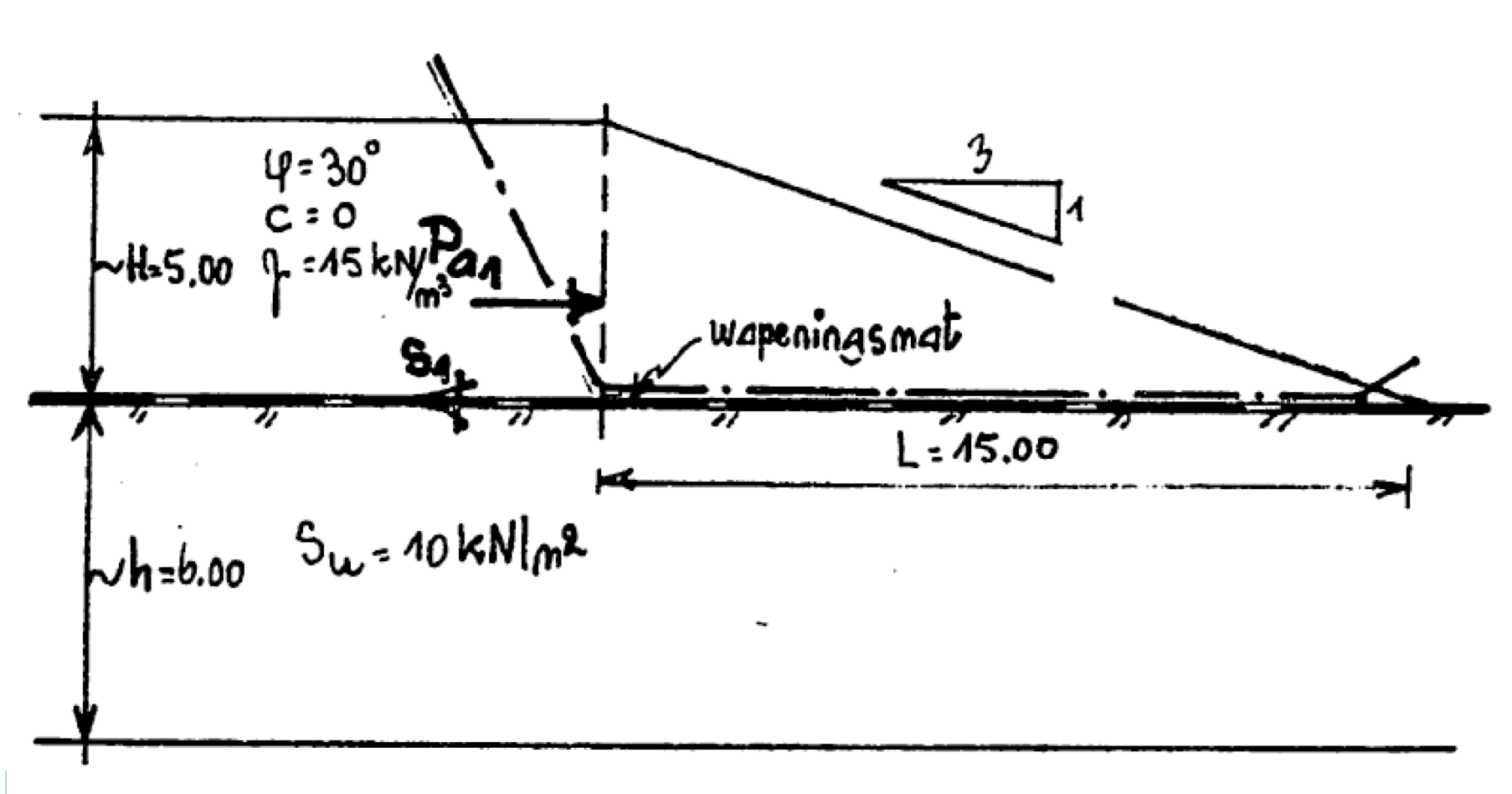
In Fig. 2 wordt een principe schets getoond uit het rapport van Risseeuw. Hierin is tevens een getallen voorbeeld aangegeven.

Doorpersen

Bij doorpersen wordt gevreesd voor stabiliteitsverlies van de ondergrond onder de helling. Het principe is geschetst in Fig. 3. Op de gearceerde grondmassa werken vier horizontale krachten, twee vaste normaalkrachten en twee gelimiteerde schuifkrachten. Aan de linker kant werkt een actieve spanning ten opzichte van de verticale, aan de rechter kant een passieve. Beide verticale spanningen liggen vast via eigen gewicht. Voor het krachten evenwicht kan dan ook geschreven worden:

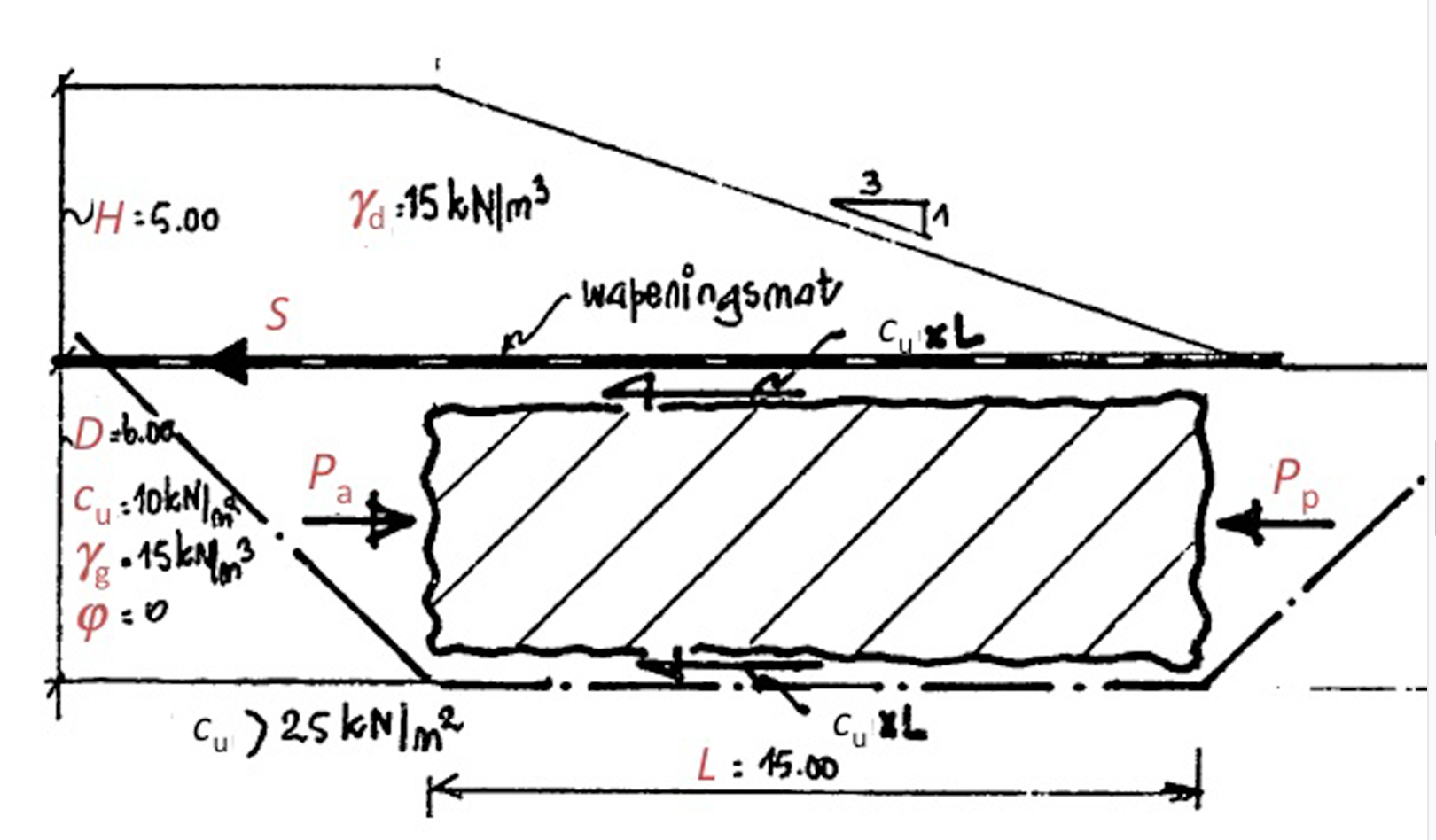
In Fig.3: schets van de ophoging met specifieke afschatting van de uitpersing

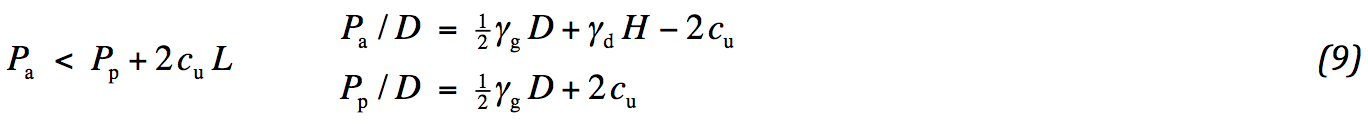
In het geval van een cohesief materiaal is de actieve spanning twee maal de waarde van de cohesie kleiner dan de corresponderende spanning. De passieve spanning is twee maal de waarde van de cohesie groter.

De schuifspanning aan de bovenzijde van de gearceerde grondmassa dient geleverd te worden door de geokunststof. De vereiste sterkte is dan:

Een veiligheidsfactor is toegevoegd.

Vereiste sterkte van de geokunststof

Er zijn drie principes besproken, waardoor een geokunststof de stabiliteit van een ophoging kan waarborgen. Voor elk principe is de vereiste sterkte bepaald op de plaats waar deze maximaal is. Deze plaatsen zullen over het algemeen niet samenvallen. Er is geen informatie bepaald om tot een gewogen afschatting te komen van de invloed van alle op het geheel. Daarom wordt gekozen voor een conservatieve aanpak door alle vereiste sterkten op te tellen.

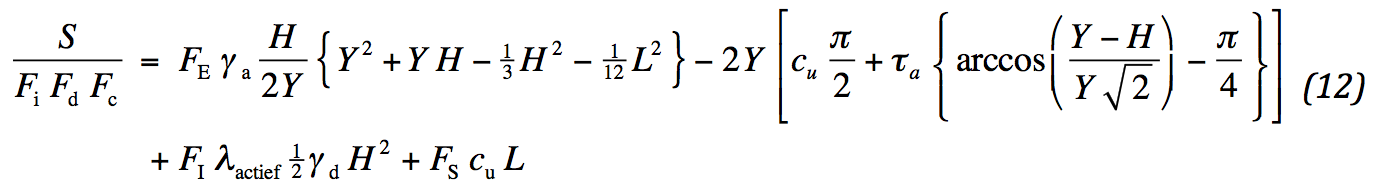
De indices voor de veiligheidsfactoren van de geokunststof slaan op i voor ‘installatie’, d voor ‘duurzaamheid’ en c voor ‘kruip’. Bij een berekening kunnen enkele uitzonderingsgevallen optreden. Deze zijn:

De 3 bezwijk mechanismen zullen niet samen en op hetzelfde tijdstip voorkomen. Daarom wordt er bekeken welke van twee combinaties de grootste sterkte van de geokunststof vereist: in elk geval het extern bezwijken en daarbij opgeteld het intern bezwijken of (niet en) het doorpersen.

Referenties

Risseeuw, P., “Rekenen met kunststof wapeningsmatten in en onder grondlichamen”, 1982.