Ontwerp van geotextielen voor toepassing onder onverharde wegen - Methode Semmmeijer

Functie van het geotextiel

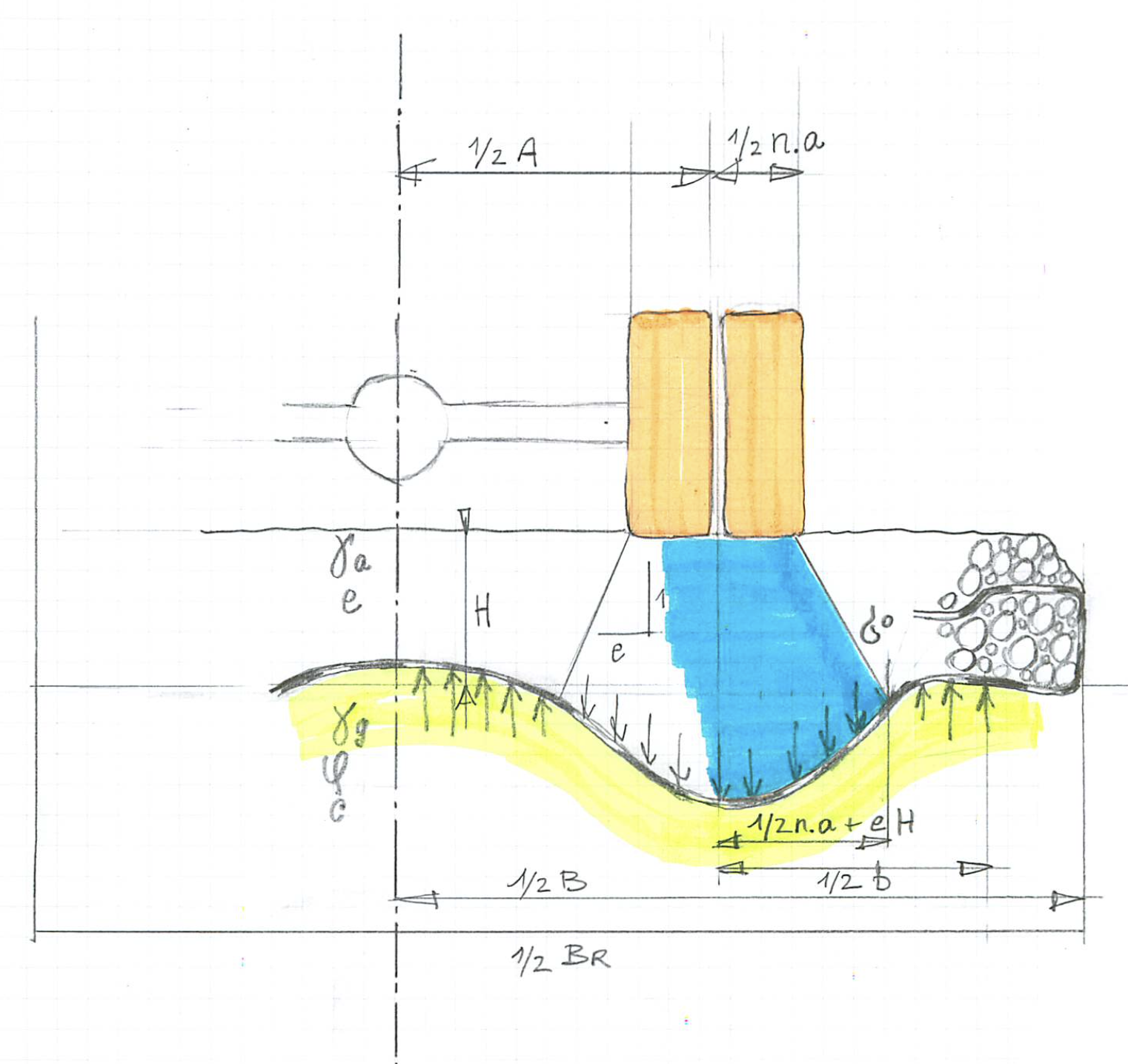
De toepassing van (wapening) geotextielen in de wegenbouw is interessant, als het draagvermogen van de ondergrond te kort schiet. De verkeerslast dreigt dan met een deel van de weg eronder weg te zakken. Een geotextiel zal de last over een groter deel van de weg spreiden, waardoor hogere aslasten mogelijk zijn bij eenzelfde draagvermogen. In Fig. 1 is dit principe geschetst. Via de banden wordt de aslast op de weg uitgeoefend. Deze spreidt in het aggregaat en oefent uiteindelijk een gemiddelde spanning σ₀ uit op de ondergrond. Het geotextiel zorgt ervoor dat deze spanning nog verder spreidt en verminderd wordt tot gemiddeld σ₁. Het ontwerp moet zodanig uitvallen dat deze laatste spanning tegemoet komt aan het draagvermogen van de ondergrond. In deze notitie zal aangegeven worden hoe dit tot stand gebracht wordt.

Werking van een geotextiel

Het gebruik van een geotextiel hier lijkt enigszins op dat van staal in gewapend beton. Het voegt de mogelijkheid van trekspanningen in het systeem toe. Het aggregaat alleen heeft hiertoe geen mogelijkheden. Een volledige analogie met gewapend beton is de toepassing die aangeven wordt met “lateral restraint”. De voor- en nadelen hiervan zijn:

- De weg zelf vervormt weinig en zou verhard kunnen worden.

- Het voertuig mag in de breedterichting van positie veranderen.

- De verbetering van het draagvermogen is beperkt, omdat de stijfheid van een geotextiel relatief slap is en navenant geen grote trekspanningen zich zullen ontwikkelen.

Een aanpak waarbij een veel grotere toename van het draagvermogen mogelijk is wordt aangegeven met “membrane action”. De voor- en nadelen hiervan zijn:

- De weg vervormt aanmerkelijk en kan beter niet verhard worden.

- Het voertuig moet steeds in hetzelfde spoor rijden, omdat op die plaats het geotextiel voorgevormd is om maximale trekkrachten te leveren.

- Geotextiel moet aan de zijkanten van de weg goed verankerd zijn.

Membraan actie

Membraan actie is een berekening, waarbij een opgespannen membraan vervormt onder de verticale spanningen die erop werken. Het geotextiel kunnen we opvatten als zo’n membraan met spanningen σ₀ en σ₁, zie de schets. De berekening zal hier beknopt worden aangestipt en de resultaten zullen worden toegelicht. Voor de oorspronkelijke publicatie wordt verwezen naar Semmmeijer et al. 1982.

Er moet een berekening worden uitgevoerd voor drie gebieden: onder de banden en de uitbreidingen links en rechts hiervan. Die gebieden hoeven niet symmetrisch te zijn, omdat het voertuig te dicht op het midden of de rand van de weg kan rijden. In die gevallen schuift de tegendruk op naar links of rechts. De gebieden geven we aan met een index i = 1 , 2 , 3 .

In elk gebied wordt de vervorming van het membraan bepaald. Daarnaast de bijbehorende verlenging en spanning. In elke oplossing zitten nog twee vrijheden. Deze zijn bepaald door aansluitingsvoorwaarden op de randen. Uiteindelijk wordt de vorm van de vervorming en het verloop van de spanningen in het geotextiel uitgedrukt in verkeerslast, draagvermogen en eigenschappen van weg en geotextiel.

De vervorming is bepaald via de membraanvergelijking: :

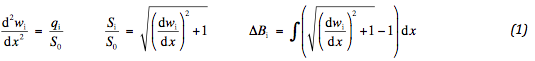
De verticale spanning q is de resultante van de boven en onderspanning op het geotextiel. De kracht in het geotextiel S heeft een constante horizontale component S₀ . De zakking is aangegeven met w en de geometrische verlenging met ΔB. Deze grootheden variëren met de afstand x vanaf de linkerrand van het spanningsgebied. De oplossing luidt:

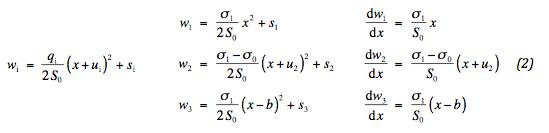
Hierin zijn de integratie constanten u_i en s_i toegevoegd. Op de randen van het spanningsgebied is geen verticale spanningscomponent aanwezig. De waarden van u₁ en u₃ zijn dus onmiddellijk bekend, omdat de helling van het geotextiel dan horizontaal is. De waarden van x op de overgangen geven we voorlopig aan met x_ℓ en x_r . Deze worden later gespecificeerd. Omdat de zakking en de helling op de overgangen moeten aansluiten, volgt er:

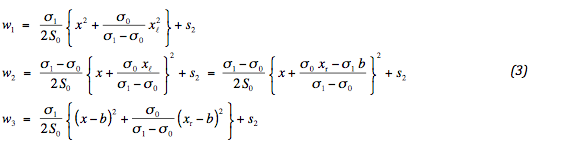
Voor de zes integratie constanten waren zes voorwaarden beschikbaar. Het blijkt dat hierdoor slechts vijf vrijheden zijn gespecificeerd. Dit komt, omdat een van de voorwaarden gebruikt is om het verticale evenwicht te verzekeren: (x_r - x_ℓ) σ₁ = b σ₀ . Dit komt tot uiting in de twee identieke vergelijkingen voor de middelste zakking. Het gevolg is, dat een absolute waarde van de zakking niet bestaat. Het systeem is intern verticaal in evenwicht op elke willekeurige verticale positie. Natuurlijk moet dit systeem aansluiten op de weg, zodanig dat het hoogst gelegen punt van het geotextiel op de oorspronkelijke hoogte blijft liggen. Hierdoor is de waarde van S₂ alsnog vastgelegd.

Het blijkt dat de mate van zakking sterk beïnvloed wordt door de kracht in het geotextiel. Hoe groter deze kracht, hoe kleiner de zakking en ook hoe kleiner de helling. Er wordt naar gestreefd deze helling voldoende klein te maken ten opzichte van 1. Dat betekent dat de kracht in het geotextiel slechts een beetje groter zal zijn dan S₀, wat blijkt uit vergelijking (1). De rek van het geotextiel kan hiermee eenvoudig worden afgeschat. De eventuele werking van schuifkrachten op het geotextiel wordt hierbij niet in aanmerking genomen. Compatibiliteit vereist dat deze rek gelijk is aan de geometrische verlenging ΔB . :

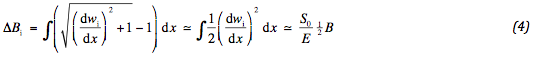
Voor de compatibiliteitsvoorwaarde wordt dan gevonden:

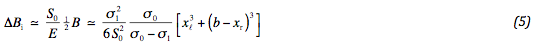
Hierin wordt de verticale evenwichtsvoorwaarde verwerkt.

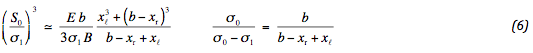
Met deze laatste voorwaarde liggen de verschilzakkingen vast. De maximale zakking in het midden is gelijk aan s₂ . Het verschil met de zakking op de randen is dan gelijk aan:

Hierin is eveneens de verticale evenwichtsvoorwaarde verwerkt.

Rekeninvoer

Om een berekening te maken zijn invoergegevens nodig. De waarde van σ₁ is gelijk aan het draagvermogen, verminderd met het gewicht van de weg. Het draagvermogen kan worden gekarakteriseerd door de schatting van Brinch Hansen. De breedte van de reactiekracht volgt dan uit de aslast:

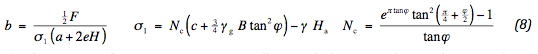
De waarden van x_ℓ en x_r worden als volgt gespecificeerd. Indien er geen beperkende voorwaarden zijn, spreidt de belasting zich vanuit de locatie van de banden. Indien de reactiekracht zich uitstrekt voorbij het midden of de rand van de weg treedt er een verschuiving op. Er geldt:

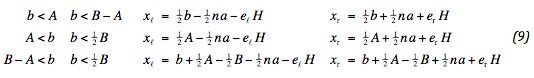
Merk op, dat aan de spanningspreiding een index is toegevoegd, ook deze spreiding is beperkt tot de weghelft. Als de spreiding hier buiten treedt wordt de waarde ervan verkleind, zodanig dat dit ongedaan gemaakt wordt. Ter controle wordt de som en het verschil van x_ℓ en x_r beschouwd:

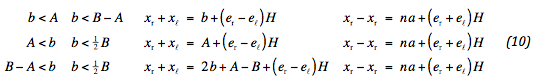
Het verschil is steeds de totale bandbreedte plus spreiding. De middenpositie komt overeen met de plaats van de aslast, aangepast aan het verschil in spreiding. De overige invoergegevens spreken voor zich.

Referenties

Semmmeijer, J.B., Kenter, C.J. and Van Den Berg, C., 1982, “Calculation Method for Fabric Reinforced Road”, Proceedings of the Second International Conference on Geotextiles, IFAI, Vol. 2, Las Vegas, Nevada, USA, August 1982, pp. 393-398.