Ontwerp van geotextiel voor toepassing onder verharde wegen - Methode Semmmeijer

Functie van geotextiel

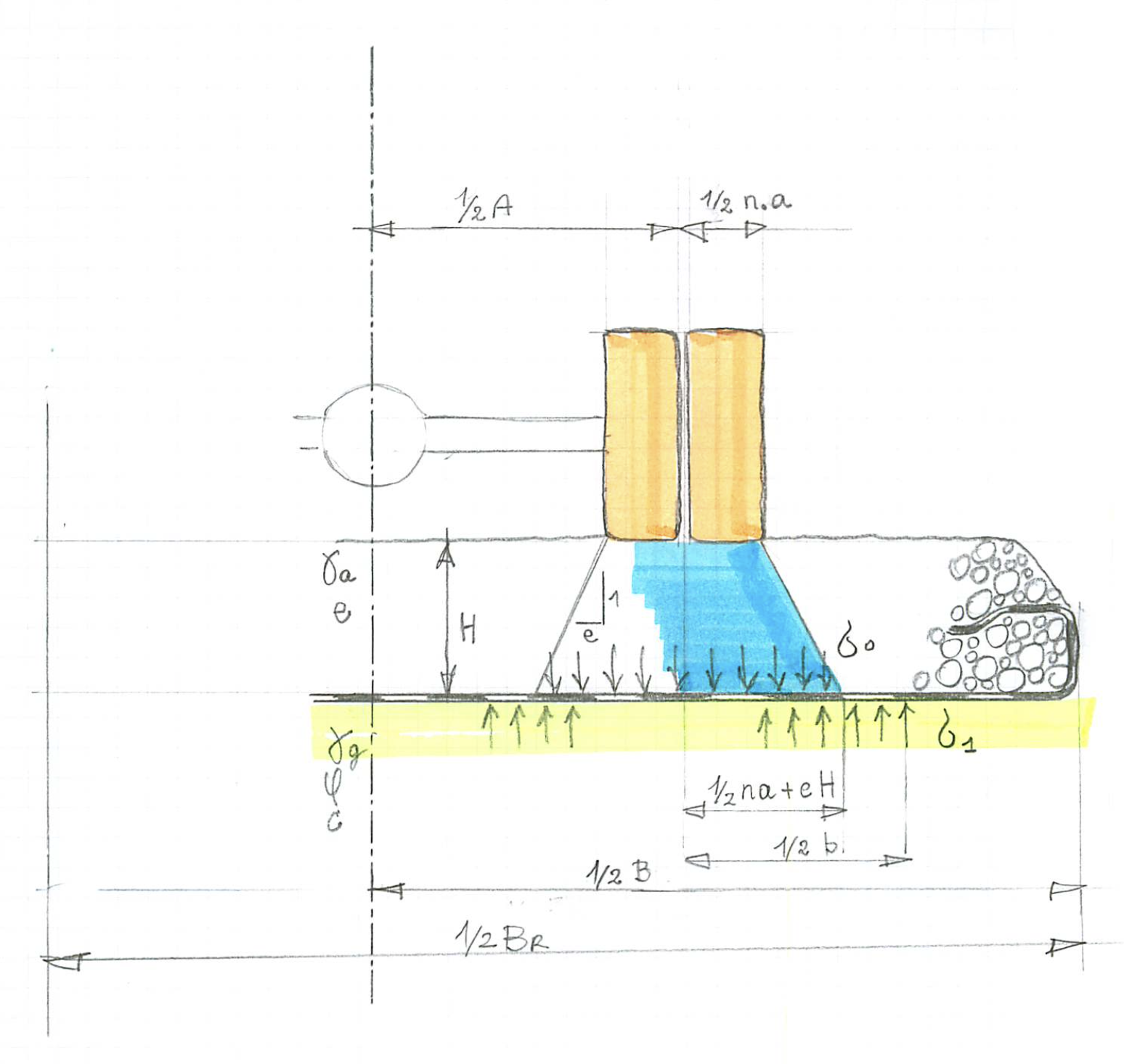
De toepassing van geotextielfen in de wegenbouw is interessant, als het draagvermogen van de ondergrond te kort schiet. De verkeerslast dreigt dan met een deel van de weg eronder weg te zakken. Een geotextiel zal de last over een groter deel van de weg spreiden, waardoor hogere aslasten mogelijk zijn bij eenzelfde draagvermogen. In Fig. 1 is dit principe geschetst. Via de wielen wordt de aslast op de weg uitgeoefend. Deze spreidt in het aggregaat. Door de geotextiel wordt deze spreiding nog verder doorgezet naar de zijkanten. Het ontwerp moet zodanig uitvallen dat deze laatste spanning tegemoet komt aan het draagvermogen van de ondergrond.

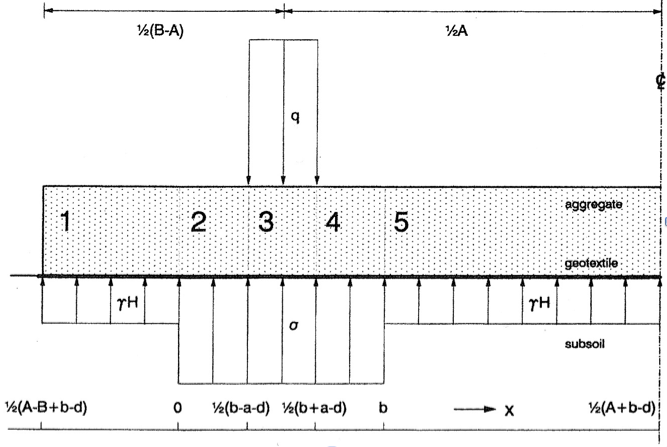
Fig. 1: Spanningen en afmetingen bij een wiellast op een wegdoorsnede

Werking van een geotextiel

Het gebruik van een geotextiel in wegconstructies lijkt enigszins op dat van staal in gewapend beton. Het voegt de mogelijkheid van trekspanningen in het systeem toe. Het aggregaat alleen heeft hiertoe geen mogelijkheden. geotextielfen kunnen toegepast worden op twee manieren. Deze worden in de literatuur aangegeven als “lateral Restraint” en “Membrane Action”. De eerste komt nog het meest overeen met gewapend beton. De voor- en nadelen hiervan zijn:

- De weg zelf vervormt weinig en zou verhard kunnen worden.

- Het voertuig mag in de breedterichting van positie veranderen.

- De verbetering van het draagvermogen is beperkt, omdat de stijfheid van een geotextiel relatief slap is en navenant geen grote trekspanningen zich zullen ontwikkelen.

Een aanpak waarbij een veel grotere toename van het draagvermogen mogelijk is wordt aangegeven met “Membrane Action”. De voor- en nadelen hiervan zijn:

- De weg vervormt aanmerkelijk en kan beter niet verhard worden.

- Het voertuig moet steeds in hetzelfde spoor rijden, omdat op die plaats het geotextiel voorgevormd is om maximale trekkrachten te leveren.

- De verbetering van het draagvermogen is nu niet meer beperkt door de stijfheid van een geotextiel, maar door zijn sterkte. Deze is veel effectiever.

- geotextiel moet aan de zijkanten van de weg goed verankerd zijn.

"Lateral Restraint"

Lateral Restraint is een aanpak, waarbij aggregaat en geotextiel interactief de verkeerslast overbrengen op de ondergrond. Dit wordt vaak aangegeven met SGA systeem (Soil-Geotextile-Aggregate). Hoe dit werkt zal hier worden aangestipt. Voor de originele publicatie wordt verwezen naar Semmmeijer 1990.

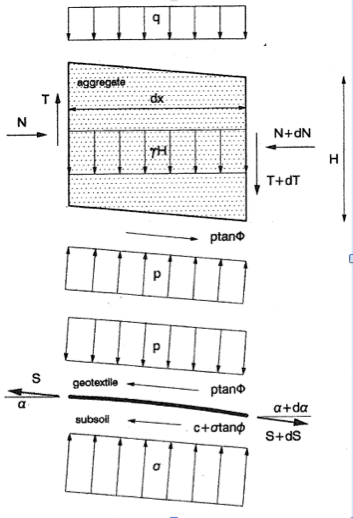
Fig. 2: Spanningen langsheen weg doorsnede

Het samenspel van spanningen op een wegelement is geschetst in Fig 2. Aggregaat en geotextiel wisselen een normaal spanning p en schuifspanning p tanΦ uit. Φ is de wrijvingshoek tussen aggregaat en kunststof. Het aggregaat is belast met een eigen gewicht γ_a H en verkeerslast q. Hierdoor ontstaat een vervorming α . Langs de zijvlakken treden een normaal kracht N en een schuif kracht T op. In de geotextiel wordt een trekkracht S opgewekt, terwijl de tegendruk van de ondergrond zich instelt op het beschikbare draagvermogen σ met schuif component c + σ tanϕ. c is de adhesie and ϕ de wrijvingshoek, beide tussen ondergrond en geotextiel. Vanwege redenen van eenvoud is de adhesie gelijkgesteld aan de cohesie van de ondergrond. De voorwaarden van horizontaal en verticaal evenwicht resulteert in een set differentiaal vergelijkingen voor zowel aggregaat als geotextiel. Voor het aggregaat luiden deze:

Voor de geotextiel luiden de voorwaarden:

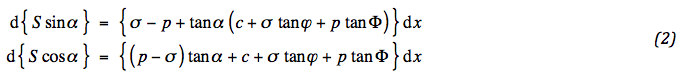
Hierin worden de differentiaties met betrekking tot S and α expliciet geschreven:

Evenwicht alleen is niet genoeg om het mechanisme van het systeem vast te leggen. Het constitutieve gedrag speelt ook een rol. De schuifspanning en vervorming zijn gerelateerd via de glijdingsmodulus van aggregaat G :

Op dit moment is er genoeg informatie om de verkregen vergelijkingen uit te werken. Door de eerste uitdrukking van (01) en (04) wordt de spanning p beschreven. Het resultaat wordt gesubstitueerd in (03) and levert twee vergelijkingen op. Deze leggen de trekkracht en vervorming vast van de geotextiel. Bovendien wordt de normaalkracht N gespecificeerd door substitutie van p in de tweede vergelijking van (01) . Het resultaat wordt uitgeschreven met een paar tussenstappen:

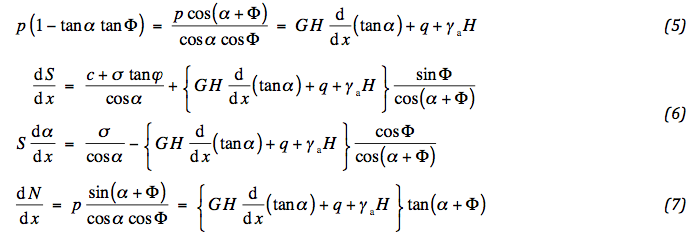
Dit is het juiste moment om de beschrijving toe te spitsen op het speciale geval van kleine vervormingen. (06) and (07) mogen bij benadering geschreven worden als:

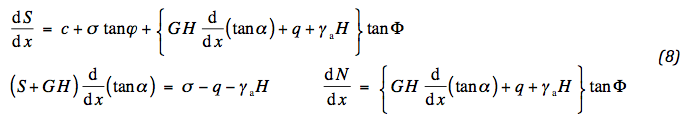
Voor kleine tot gematigde deformaties is the parameter G H van veel grotere orde dan de trekkracht S . De volgende set van ontkoppelde vergelijkingen resulteert:

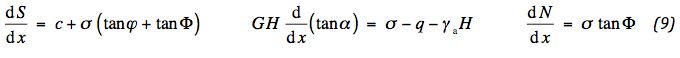
Uit deze vergelijkingen blijkt dat de vervorming in belangrijke mate beheerst wordt door de stijfheid van het aggregaat. De trekkracht in de geotextiel draagt bij door drukkrachten op te wekken in het aggregaat, waardoor de gemobiliseerde wrijving binnen de perken blijft.

De modelleringfase is nu klaar, ofschoon nog niet alle grootheden gespecificeerd zijn. Het concept van gemobiliseerde wrijving en de vervorming van het geotextiel zullen nog moeten worden uitgewerkt.

Ontwerp

Het model wordt toegepast op de actuele situatie van Fig. 1. B is de medewerkende breedte van de weg; A de asbreedte van het voertuig; a de breedte van het wiel met n banden en verkeerslast q ; b is de breedte van het draagvermogen σ, welke volgt uit het verticale evenwicht: b ( σ - γ_a H ) = n a q . Als de asbreedte te smal is of het voertuig te dicht op de rand van de weg rijdt, verschuift de grondreactie over een afstand d. De volgende situaties zijn mogelijk:

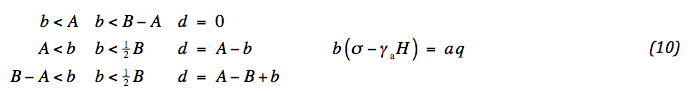
In Fig. 1 is aangegeven dat er 5 secties met verschillende belasting toestand worden onderscheiden. Secties 1 en 5 vertonen geen vervorming, omdat de tegendruk van de ondergrond het eigen gewicht van de weg compenseert. In secties 2 and 4 is de vervorming convex ten gevolge van de belasting σ – γ.H ; in sectie 3 concaaf ten gevolge van de belasting q – σ – γ.H . Dit kan worden nagegaan met behulp van de tweede vergelijking van (09), waardoor de vervorming bepaald is. In het concept van gemobiliseerde wrijving speelt de schuifkracht een belangrijke rol. Deze hangt volgens (04) af van de vervorming. Integratie van de tweede vergelijking van (09) is recht toe recht aan. Per sectie is de vervorming lineair en continu op de overgangen. De grootste vervorming treedt op in de overgangen van sectie 2 naar 3 en van 3 naar 4. Substitutie ervan in (04) leidt tot de volgende maximale schuifkrachten:

Omdat dw/dx = tanα, volgt de verticale verplaatsing w door de vervorming te integreren. Deze is per sectie kwadratisch. Het maximale verschil tussen de locatie onder het wiel en de rand of het midden van de weg blijkt dan te zijn:

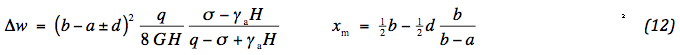
x_m is de positie onder het wiel. De verticale verplaatsing blijkt vooral af te hangen van de stijfheid van het aggregaat. Merk echter op, dat deze stijfheid sterk afneemt door plastische vervorming, wat weer beïnvloed wordt door de kwaliteit van de geotextiel. Dit wordt later nog toegelicht.

De volgende fase in de berekening is het bepalen van de normaalkracht in het aggregaat. Deze is bepaald door de derde vergelijking van (09). Integratie is weer recht toe recht aan. Merk op dat de richting van de schuifspanning links en rechts van x = x_m tegengesteld is. Voorts is de ontwikkeling van schuifspanning direct onder de wielen twijfelachtig en daarom weggelaten. De maximale normaalkracht wordt aangegeven met N_m . Deze treedt onder de wielen op. De volgende uitdrukkingen zijn bepaald:

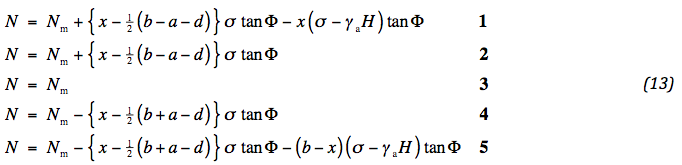
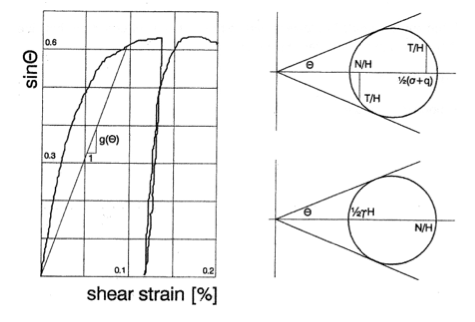
Fig. 3: Gemobiliseerde wrijving

De vet gedrukte cijfers verwijzen naar de secties. De waarde van N_m is bepaald door de mate van gemobiliseerde wrijving. Deze is bepaald door de verhouding van deviatorische en isotrope spanning. Er zijn twee posities waar een maatgevende waarde voor de hand ligt: onder het wiel en naast de reactie van de ondergrond. In het eerste geval ligt deze vast door de gemiddelde verticale spanning ½ ( σ + q ) , de horizontale spanning N_m / H en de schuifspanning T_m / H ; in het laatste geval door de gemiddelde verticale spanning ½ γ_a H and de horizontale spanning { N_m – ½ ( b - a ± d ) σ tan Φ }. In Fig. 3 zijn hiervoor de bijbehorende cirkels van Mohr getekend. Er kan worden afgelezen:

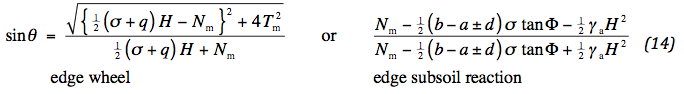
Met behulp van (11) kan een expliciete uitdrukking voor N_m worden opgesteld. Het gaat om een zo groot mogelijke waarde van θ, zodat de absolute waarde van d moet worden gehanteerd. De volgende alternatieven worden verkregen:

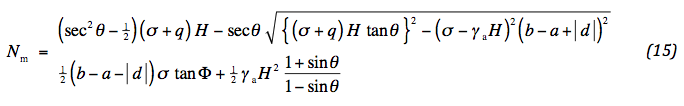
In principe is de bovenste waarde maatgevend. Maar het zou zo maar kunnen, dat de onderste waarde dan overschreden wordt. Daarom moet in een ontwerp altijd gecontroleerd worden, dat de onderste waarde gehaald kan worden. Wel moet er nog op gelet worden dat de discriminant positief blijft. Dit is het geval, als:

Hieruit blijkt dat de dikte van de weg niet te klein gekozen kan worden. Anders plooit de weg op door te sterke trekkrachten in het aggregaat. Ook blijkt, dat het in dit opzicht gunstig is om in het ontwerp een waarde d ≠ 0 af te regelen.

Zonder voertuig zit er al een horizontale normaalkracht in het aggregaat ten gevolge van het eigen gewicht. Deze kracht geven we aan met N₀ . De waarde ervan zal later worden afgeschat. Nu is het mogelijk dat de waarde van N aan een van de zijkanten lager dreigt te worden dan N₀ . Dan houdt simpelweg de activiteit van de kunststof op. Dit betekent dat de werkzame breedte van de weg versmald moet worden. Zo dadelijk geldt eenzelfde probleem voor de trekkracht in de kunststof. Dat speelt zich af op het midden van de weg. Daarom kijken we nu eerst naar de zijkant van de weg.

Het is nu mogelijk voor de versmalling een uitdrukking op te stellen. De waarde van x op de zijkant van de weg, ½ (A - B + b - d) zie Fig. 1, wordt ingevuld in de normaalkracht van sectie 1. Door de zijkant dichterbij te leggen wordt voldaan aan de grootte van het invloedsgebied:

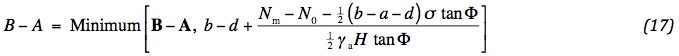
De vetgedrukte grootheden zijn de originele. Met de aangepaste waarde zal verder worden gerekend. De waarde van de normaalkracht op de rand luidt:

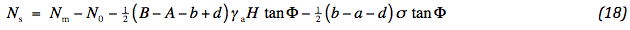
Nu wordt de aandacht gericht op de trekkracht in de geotextiel, vastgelegd via de eerste vergelijking van (9). Dezelfde opmerkingen als gemaakt voor de normaalkracht zijn hier van kracht. De maximale trekkracht wordt aangegeven met S_m. De volgende uitdrukkingen zijn bepaald:

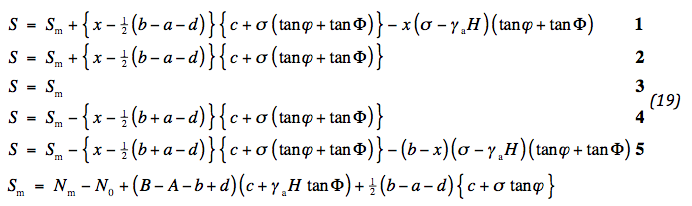
De waarde van S_m volgt uit het gelijkstellen van normaalkracht en trekkracht op de zijkant van de weg. Nu is er een kans dat de trekkracht nul wordt in het midden van de weg. Dan kan dezelfde remedie worden aangewend als eerder bij de normaalkracht. De afstand van wiel tot midden van de weg wordt dan aangepast:

Zolang de trekkracht positief is, is de normaalkracht dat ook. De laatste fase van de berekening betreft de compatibiliteit van de rekken. Direct onder het wiel wordt het aggregaat verondersteld plastisch te zijn. Hierdoor wordt het aggregaat naar buiten geduwd, waardoor de geotextiel rekt. De rek is evenredig met de trekkracht:

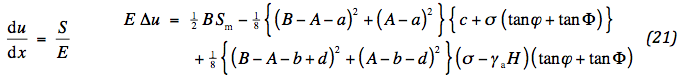
E is de Young modulus van de kunststof. Integratie is toegepast op (19). Voor een toelaatbare verplaatsing ligt de waarde van E direct vast. Rek in het aggregaat is alleen van belang onder de wielen, waar het gedrag plastisch is. Elastische vervormingen elders zijn veel en veel kleiner en worden verwaarloosd. Volgens de spanning-rek theorie hangen de rekken af van zowel de horizontale als verticale spanning, gewogen via de dwarscontractie coëfficiënt:

σ_v is the gemiddelde verticale spanning. Onder het wiel is de spanningstoestand constant. Voor de verplaatsing wordt dan gevonden:

Ook hier ligt voor een toelaatbare verplaatsing de waarde van de G direct vast. Deze waarde kan zich door het plastische gedrag automatisch instellen. Wat rest is een faire keuze voor N₀. Als compromis kiezen we een waarde die de rek ten gevolge van het eigen gewicht van het aggregaat opheft. Deze wordt bepaald analoog aan (22):

Dit is slechts een keuze en wellicht een onderwerp voor toekomstig onderzoek.

Plastisch gedrag van het aggregaat

In de vorige paragrafen is een model afgeleid om een weg te versterken met behulp van een geotextiel. Hierin is het aggregaat direct onder het wiel verondersteld plastisch te reageren. Hierdoor kan zich in de kunststof een trekkracht ontwikkelen, waardoor het gehele SGA systeem hogere verkeerslasten aan kan.

Tijdens dit plastisch vervormen wordt een horizontale vervorming toegelaten, welke met de juiste stijfheid van de kunststof voor de vereiste wapening zorgt. Hierbij daalt de stijfheid van het aggregaat zodanig dat zich hierin de bijbehorende normaalkrachten ontwikkelen. Het enige, waarop hierbij gelet moet worden, is de vraag of de elastische uitgangswaarde voldoende groot is. Een toename is natuurlijk uitgesloten. Valstad en Strøm (1976) hebben via experimenten een schatting gemaakt van de elastische stijfheid van aggregaat. Hiervoor hebben ze de volgende relatie voorgesteld:

G_t en p_t zijn de stijfheid en de isotrope spanning in het experiment. g(θ) is de secant modulus in Fig. 3, welke kleiner wordt met de mate van schuifvervorming. De werkelijke stijfheid hangt af van de actuele isotrope spanning. De waarde hiervan is ingevuld in formule (25). β is een macht die de niet-lineariteit weergeeft. De waarde hiervan ligt rond de 0,5.

Samenvatting

Het model is nu klaar en kan worden toegepast. Het is handig de vereiste formules te groeperen. Zij zijn gekopieerd van (10), (15), (17), (19), (21), (23) en (24):

Eerst wordt de normaalkracht bepaald. Hiervoor zijn twee uitdrukkingen afgeleid. De bovenste is maatgevend, mits de onderste geen beperkingen oplevert. Dit moet altijd even gecontroleerd worden. Meestal is de onderste waarde zelfs groter dan de bovenste, wat ruimschoots voldoet.

Vervolgens wordt de medewerkende breedte vanaf de zijkant eventueel aangepast. Hierna volgt de bepaling van de trekkracht met een eventuele aanpassing van de medewerkende breedte in het midden van de weg. Tenslotte volgen de vereiste stijfheid voor de kunststof en de aangepaste stijfheid voor het aggregaat. Het draagvermogen kan worden gekarakteriseerd door de schatting van Brinch Hansen:

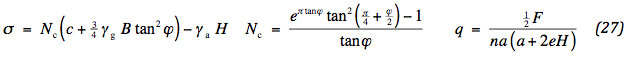
Voor de volledigheid is de relatie tussen aslast en spanning onder het wiel toegevoegd.

Referenties

Semmmeijer, J.B., 1990, “Design of Geotextile Reinforced Paved Roads and Parking Areas”, Proceedings of the Fourth International Conference on Geotextiles, Geomembranes and Related Products, Balkema, Vol. 1, The Hague, The Netherlands, pp.177-182.

Valstad, T. and Strøm, E. , “Investigations of the Mechanical Properties of Rockfill for the Svartevann Dam, using Triaxial, Oedometer and Plate Bearing Tests”, Norges Geotek. Inst. , Publ. 110, pp 3-8.